|
libalmath
2.4.3.28-r2
|
|
libalmath
2.4.3.28-r2
|
Classes | |
| struct | AL::Math::Pose2D |
| A pose in a 2-dimentional space. More... | |
| struct | AL::Math::Position2D |
| Create and play with a Position2D. More... | |
| struct | AL::Math::Position3D |
| Create and play with a Position3D. More... | |
| struct | AL::Math::Position6D |
| Create and play with a Position6D. More... | |
| struct | AL::Math::PositionAndVelocity |
| Create and play with a PositionAndVelocity. More... | |
| struct | AL::Math::Quaternion |
| Create and play with a Quaternion. More... | |
| struct | AL::Math::Rotation |
| A 3*3 rotation matrix. More... | |
| struct | AL::Math::Rotation3D |
| A Rotation3D give 3 composed angles in radians. More... | |
| struct | AL::Math::Transform |
| A homogenous transformation matrix. More... | |
| struct | AL::Math::Velocity3D |
| Create and play with a Velocity3D. More... | |
| struct | AL::Math::Velocity6D |
| Create and play with a Velocity6D. More... | |
Typedefs | |
| typedef std::bitset< 6 > | AL::Math::AXIS_MASK |
| Definition of an AXIS_MASK as a bit set. More... | |
Functions | |
| std::ostream & | AL::Math::operator<< (std::ostream &pStream, const Pose2D &pPos) |
| Overloading of operator << for Pose2D. More... | |
| std::ostream & | AL::Math::operator<< (std::ostream &pStream, const Position2D &pPos) |
| Overloading of operator << for Position2D. More... | |
| std::ostream & | AL::Math::operator<< (std::ostream &pStream, const Position3D &pPos) |
| Overloading of operator << for Position3D. More... | |
| std::ostream & | AL::Math::operator<< (std::ostream &pStream, const Position6D &pPos) |
| Overloading of operator << for Position6D. More... | |
| std::ostream & | AL::Math::operator<< (std::ostream &pStream, const PositionAndVelocity &pPosVel) |
| Overloading of operator << for PositionAndVelocity. More... | |
| std::ostream & | AL::Math::operator<< (std::ostream &pStream, const Rotation &pRot) |
| Overloading of operator << for Rotation. More... | |
| std::ostream & | AL::Math::operator<< (std::ostream &pStream, const Rotation3D &pRot) |
| Overloading of operator << for Rotation3D. More... | |
| std::ostream & | AL::Math::operator<< (std::ostream &pStream, const Transform &pT) |
| Overloading of operator << for Transform. More... | |
| std::ostream & | AL::Math::operator<< (std::ostream &pStream, const TransformAndVelocity6D &pTV) |
| Overloading of operator << for TransformAndVelocity6D. More... | |
| std::ostream & | AL::Math::operator<< (std::ostream &pStream, const Velocity3D &pVel) |
| Overloading of operator << for Velocity3D. More... | |
| std::ostream & | AL::Math::operator<< (std::ostream &pStream, const Quaternion &pQua) |
| Overloading of operator << for Quaternion. More... | |
| std::ostream & | AL::Math::operator<< (std::ostream &pStream, const Velocity6D &pVel) |
| Overloading of operator << for Velocity6D. More... | |
| std::string | AL::Math::toSpaceSeparated (const Position3D &pPos) |
| Create a string of Position3D. More... | |
| std::string | AL::Math::toSpaceSeparated (const Rotation3D &pPos) |
| Create a string of Rotation3D. More... | |
| std::string | AL::Math::toSpaceSeparated (const Velocity6D &pVel) |
| Create a string of Velocity6D. More... | |
| std::string | AL::Math::toSpaceSeparated (const Transform &pT) |
| Create a string of Transform. More... | |
| std::string | AL::Math::toSpaceSeparated (const Position6D &pPos) |
| Create a string of Position6D. More... | |
| std::string | AL::Math::toSpaceSeparated (const Quaternion &pQuat) |
| Create a string of Quaternion. More... | |
| float | AL::Math::distanceSquared (const Pose2D &pPos1, const Pose2D &pPos2) |
| Compute the squared distance between two Pose2D. More... | |
| float | AL::Math::distance (const Pose2D &pPos1, const Pose2D &pPos2) |
| Compute the distance between two Pose2D. More... | |
| void | AL::Math::pose2dInvertInPlace (Pose2D &pPos) |
| Inverse the given Pose2D in place: More... | |
| Pose2D | AL::Math::pinv (const Pose2D &pPos) |
| Alternative name for inverse: return the pose2d inverse of the given Pose2D. More... | |
| Pose2D | AL::Math::pose2dDiff (const Pose2D &pPos1, const Pose2D &pPos2) |
| Compute the Pose2D between the actual Pose2D and the one give in argument result: More... | |
| Pose2D | AL::Math::pose2DInverse (const Pose2D &pPos) |
| Compute the inverse of a Pose2D. More... | |
| void | AL::Math::pose2DInverse (const Pose2D &pPos, Pose2D &pRes) |
| Compute the inverse of a Pose2D. More... | |
| float | AL::Math::distanceSquared (const Position2D &pPos1, const Position2D &pPos2) |
| Compute the squared distance between two Position2D. More... | |
| float | AL::Math::distance (const Position2D &pPos1, const Position2D &pPos2) |
Compute the distance between two Position2D 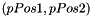 : More... : More... | |
| float | AL::Math::norm (const Position2D &pPos) |
| Compute the norm of a Position2D. More... | |
| Position2D | AL::Math::normalize (const Position2D &pPos) |
| Normalize a Position2D. More... | |
| float | AL::Math::crossProduct (const Position2D &pPos1, const Position2D &pPos2) |
| Compute the cross Product of two Position2D. More... | |
| void | AL::Math::crossProduct (const Position2D &pPos1, const Position2D &pPos2, float &pRes) |
| Compute the cross Product of two Position2D. More... | |
| bool | AL::Math::Position3D::isUnitVector (const float &pEpsilon=0.0001f) const |
| Checks if the norm of the Position3D is near to 1.0 More... | |
| bool | AL::Math::Position3D::isOrthogonal (const Position3D &pPos, const float &pEpsilon=0.0001f) const |
| Checks if this Position3D is orthogonal to Position3D pPos More... | |
| float | AL::Math::distanceSquared (const Position3D &pPos1, const Position3D &pPos2) |
| Compute the squared distance between two Position3D: More... | |
| float | AL::Math::distance (const Position3D &pPos1, const Position3D &pPos2) |
| Compute the distance between two Position3D: More... | |
| float | AL::Math::norm (const Position3D &pPos) |
| Compute the norm of a Position3D: More... | |
| Position3D | AL::Math::normalize (const Position3D &pPos) |
| Normalize a Position3D: More... | |
| bool | AL::Math::isUnitVector (const Position3D &pPos, const float &pEpsilon=0.0001f) |
| Checks if the norm of a Position3D is near to 1.0 More... | |
| bool | AL::Math::isOrthogonal (const Position3D &pPos1, const Position3D &pPos2, const float &pEpsilon=0.0001f) |
| Checks if two Position3D are orthogonal More... | |
| float | AL::Math::distanceSquared (const Position6D &pPos1, const Position6D &pPos2) |
| Compute the squared distance of translation part (x, y and z) between two Position6D: More... | |
| float | AL::Math::distance (const Position6D &pPos1, const Position6D &pPos2) |
| Compute the distance of translation part (x, y and z) between two Position6D: More... | |
| float | AL::Math::norm (const Position6D &pPos) |
| Compute the norm of a Position6D: More... | |
| Position6D | AL::Math::normalize (const Position6D &pPos) |
| Normalize a Position6D: More... | |
| float | AL::Math::norm (const Quaternion &pQua) |
| Compute the norm of a Quaternion: More... | |
| Quaternion | AL::Math::normalize (const Quaternion &pQua) |
| Normalize a Quaternion: More... | |
| void | AL::Math::quaternionInverse (const Quaternion &pQua, Quaternion &pQuaOut) |
| Return the quaternion inverse of the given Quaternion: More... | |
| Quaternion | AL::Math::quaternionInverse (const Quaternion &pQua) |
| Return the quaternion inverse of the given Quaternion More... | |
| Quaternion | AL::Math::quaternionFromAngleAndAxisRotation (const float pAngle, const float pAxisX, const float pAxisY, const float pAxisZ) |
| Create a Quaternion initialized with explicit angle and axis rotation. More... | |
| void | AL::Math::angleAndAxisRotationFromQuaternion (const Quaternion &pQuaternion, float &pAngle, float &pAxisX, float &pAxisY, float &pAxisZ) |
| Compute angle and axis rotation from a Quaternion. More... | |
| std::vector< float > | AL::Math::angleAndAxisRotationFromQuaternion (const Quaternion &pQuaternion) |
| Compute angle and axis rotation from a Quaternion. More... | |
| Rotation | AL::Math::transpose (const Rotation &pRot) |
| Compute the transpose rotation of the one given in argument: More... | |
| float | AL::Math::determinant (const Rotation &pRot) |
| Compute the determinant of the given Rotation: More... | |
| void | AL::Math::normalizeRotation (Rotation &pRot) |
| Normalize data, if needed, to have Rotation properties. More... | |
| Rotation | AL::Math::rotationFromQuaternion (const float pA, const float pB, const float pC, const float pD) |
| Creates a 3*3 Rotation Matrix from a normalized quaternion ( |a + bi + cj + dk| = 1). More... | |
| Rotation | AL::Math::rotationFromAngleDirection (const float pAngle, const float pX, const float pY, const float pZ) |
| Creates a 3*3 Rotation Matrix from a an angle and a normalized direction( |pX, pY, pZ| = 1). More... | |
| void | AL::Math::applyRotation (const AL::Math::Rotation &pRot, float &pX, float &pY, float &pZ) |
| Apply Rotation to a 3D point. More... | |
| Rotation | AL::Math::rotationFromRotX (const float pRotX) |
| Create a Rotation initialized with explicit rotation around x axis. More... | |
| Rotation | AL::Math::rotationFromRotY (const float pRotY) |
| Create a Rotation initialized with explicit rotation around y axis. More... | |
| Rotation | AL::Math::rotationFromRotZ (const float pRotZ) |
| Create a Rotation initialized with explicit rotation around z axis. More... | |
| Rotation | AL::Math::rotationFrom3DRotation (const float &pWX, const float &pWY, const float &pWZ) |
| Create a Rotation initialized with euler angle. Rot = fromRotZ(pWZ)*fromRotY(pWY)*fromRotX(pWX) More... | |
| float | AL::Math::norm (const Rotation3D &pRot) |
| Compute the norm of a Rotation3D: More... | |
| void | AL::Math::transformPreMultiply (const Transform &pT, Transform &pTOut) |
| pTOut = pT*pTOut More... | |
| float | AL::Math::norm (const Transform &pT) |
| Compute the norm translation part of the actual Transform: More... | |
| void | AL::Math::normalizeTransform (Transform &pT) |
| Normalize data, if needed, to have transform properties. More... | |
| void | AL::Math::transformToFloatVector (const Transform &pT, std::vector< float > &pTOut) |
| DEPRECATED: Use toVector function. Copy the Transform in a vector of float: More... | |
| std::vector< float > | AL::Math::transformToFloatVector (const Transform &pT) |
| DEPRECATED: Use toVector function. Return the Transform in a vector of float: More... | |
| float | AL::Math::determinant (const Transform &pT) |
| Compute the determinant of rotation part of the given Transform: More... | |
| float | AL::Math::determinant (const std::vector< float > &pFloats) |
| Compute the determinant of rotation part of the given vector of floats: More... | |
| void | AL::Math::transformInverse (const Transform &pT, Transform &pTOut) |
| Return the transform inverse of the given Transform: More... | |
| Transform | AL::Math::transformInverse (const Transform &pT) |
| Return the transform inverse of the given Transform: More... | |
| Transform | AL::Math::transformFromRotX (const float pRotX) |
| Create a Transform initialize with explicit rotation around x axis: More... | |
| Transform | AL::Math::transformFromRotY (const float pRotY) |
| Create a Transform initialize with explicit rotation around y axis: More... | |
| Transform | AL::Math::transformFromRotZ (const float pRotZ) |
| Create a Transform initialize with explicit rotation around z axis: More... | |
| Transform | AL::Math::transformFrom3DRotation (const float &pWX, const float &pWY, const float &pWZ) |
| Create a Transform initialize with euler angle: H = fromRotZ(pWZ)*fromRotY(pWY)*fromRotX(pWX) More... | |
| Transform | AL::Math::transformFromPosition (const float &pX, const float &pY, const float &pZ) |
| Create a Transform initialize with explicit value for translation part: More... | |
| Transform | AL::Math::transformFromPosition (const float &pX, const float &pY, const float &pZ, const float &pWX, const float &pWY, const float &pWZ) |
| Create a Transform initialize with explicit value for translation part and euler angle: More... | |
| void | AL::Math::transformInvertInPlace (Transform &pT) |
| Inverse the given Transform in place: More... | |
| Transform | AL::Math::pinv (const Transform &pT) |
| Alternative name for inverse: return the transform inverse of the given Transform: More... | |
| Transform | AL::Math::transformDiff (const Transform &pT1, const Transform &pT2) |
| Compute the Transform between the actual Transform and the one give in argument result: More... | |
| float | AL::Math::transformDistanceSquared (const Transform &pT1, const Transform &pT2) |
| Compute the squared distance between the actual Transform and the one give in argument (translation part): More... | |
| float | AL::Math::transformDistance (const Transform &pT1, const Transform &pT2) |
| Compute the distance between the actual Transform and the one give in argument: More... | |
| float | AL::Math::norm (const Velocity3D &pVel) |
| Compute the norm of a Velocity3D: More... | |
| Velocity3D | AL::Math::normalize (const Velocity3D &pVel) |
| Normalize a Velocity3D: More... | |
| float | AL::Math::norm (const Velocity6D &pVel) |
| Compute the norm of a Velocity6D: More... | |
| Velocity6D | AL::Math::normalize (const Velocity6D &pVel) |
| Normalize a Velocity6D: More... | |
Types classes provide many usefull defintion in robotics field such as homogenous transform matrix, 6D vector of velocty and so on.
| typedef std::bitset<6> AL::Math::AXIS_MASK |
Definition of an AXIS_MASK as a bit set.
static const int AXIS_MASK_X = 1
static const int AXIS_MASK_Y = 2
static const int AXIS_MASK_XY = 3
static const int AXIS_MASK_Z = 4
static const int AXIS_MASK_WX = 8
static const int AXIS_MASK_WY = 16
static const int AXIS_MASK_WZ = 32
static const int AXIS_MASK_WYWZ = 48
static const int AXIS_MASK_ALL = 63
static const int AXIS_MASK_VEL = 7
static const int AXIS_MASK_ROT = 56
static const int AXIS_MASK_NONE = 0
static const int AXIS_MASK_PLANEZ = 28
Definition at line 35 of file alaxismask.h.
| void AL::Math::angleAndAxisRotationFromQuaternion | ( | const Quaternion & | pQuaternion, |
| float & | pAngle, | ||
| float & | pAxisX, | ||
| float & | pAxisY, | ||
| float & | pAxisZ | ||
| ) |
Compute angle and axis rotation from a Quaternion.
| pQuaternion | the given quaternion |
| pAngle | the computed float value for angle in radian around axis rotation |
| pAxisX | the computed float value for x value of axis rotation |
| pAxisY | the computed float value for y value of axis rotation |
| pAxisZ | the computed float value for z value of axis rotation |
| std::vector<float> AL::Math::angleAndAxisRotationFromQuaternion | ( | const Quaternion & | pQuaternion | ) |
Compute angle and axis rotation from a Quaternion.
| pQuaternion | the given quaternion |
| void AL::Math::applyRotation | ( | const AL::Math::Rotation & | pRot, |
| float & | pX, | ||
| float & | pY, | ||
| float & | pZ | ||
| ) |
Apply Rotation to a 3D point.
| pRot | the given rotation |
| pX | the X position of the 3D point after rotation |
| pY | the Y position of the 3D point after rotation |
| pZ | the Z position of the 3D point after rotation |
| float AL::Math::crossProduct | ( | const Position2D & | pPos1, |
| const Position2D & | pPos2 | ||
| ) |
Compute the cross Product of two Position2D.
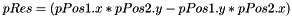
| pPos1 | the first Position2D |
| pPos2 | the second Position2D |
| void AL::Math::crossProduct | ( | const Position2D & | pPos1, |
| const Position2D & | pPos2, | ||
| float & | pRes | ||
| ) |
Compute the cross Product of two Position2D.
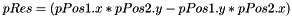
| pPos1 | the first Position2D |
| pPos2 | the second Position2D |
| pRes | the float cross product between the two Position2D |
| float AL::Math::determinant | ( | const Rotation & | pRot | ) |
| float AL::Math::determinant | ( | const Transform & | pT | ) |
| float AL::Math::determinant | ( | const std::vector< float > & | pFloats | ) |
Compute the determinant of rotation part of the given vector of floats:
![$pT[0]*pT[5]*pT[10] + pT[1]*pT[6]*pT[8] + pT[2]*pT[4]*pT[9] - pT[0]*pT[6]*pT[9] - pT[1]*pT[4]*pT[10] - pT[2]*pT[5]*pT[8]$](form_88.png)
| pFloats | the given vector of floats |
| float AL::Math::distance | ( | const Position2D & | pPos1, |
| const Position2D & | pPos2 | ||
| ) |
Compute the distance between two Position2D 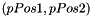 :
:
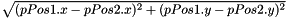
| pPos1 | the first Position2D |
| pPos2 | the second Position2D |
| float AL::Math::distance | ( | const Position3D & | pPos1, |
| const Position3D & | pPos2 | ||
| ) |
Compute the distance between two Position3D:
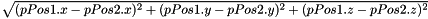
| pPos1 | the first Position3D |
| pPos2 | the second Position3D |
| float AL::Math::distance | ( | const Position6D & | pPos1, |
| const Position6D & | pPos2 | ||
| ) |
Compute the distance of translation part (x, y and z) between two Position6D:
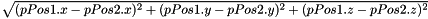
| pPos1 | the first Position6D |
| pPos2 | the second Position6D |
| float AL::Math::distance | ( | const Pose2D & | pPos1, |
| const Pose2D & | pPos2 | ||
| ) |
| float AL::Math::distanceSquared | ( | const Position2D & | pPos1, |
| const Position2D & | pPos2 | ||
| ) |
Compute the squared distance between two Position2D.
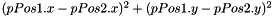
| pPos1 | the first Position2D |
| pPos2 | the second Position2D |
| float AL::Math::distanceSquared | ( | const Position3D & | pPos1, |
| const Position3D & | pPos2 | ||
| ) |
Compute the squared distance between two Position3D:
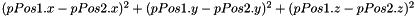
| pPos1 | the first Position3D |
| pPos2 | the second Position3D |
| float AL::Math::distanceSquared | ( | const Position6D & | pPos1, |
| const Position6D & | pPos2 | ||
| ) |
Compute the squared distance of translation part (x, y and z) between two Position6D:
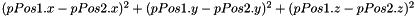
| pPos1 | the first Position6D |
| pPos2 | the second Position6D |
| float AL::Math::distanceSquared | ( | const Pose2D & | pPos1, |
| const Pose2D & | pPos2 | ||
| ) |
| bool AL::Math::Position3D::isOrthogonal | ( | const Position3D & | pPos, |
| const float & | pEpsilon = 0.0001f |
||
| ) | const |
Checks if this Position3D is orthogonal to Position3D pPos
| pEpsilon | an optional epsilon distance |
| bool AL::Math::isOrthogonal | ( | const Position3D & | pPos1, |
| const Position3D & | pPos2, | ||
| const float & | pEpsilon = 0.0001f |
||
| ) |
Checks if two Position3D are orthogonal
| pPos1 | the first Position3D |
| pPos2 | the second Position3D |
| pEpsilon | an optional epsilon distance |
| bool AL::Math::Position3D::isUnitVector | ( | const float & | pEpsilon = 0.0001f | ) | const |
Checks if the norm of the Position3D is near to 1.0
| pEpsilon | an optional epsilon distance |
| bool AL::Math::isUnitVector | ( | const Position3D & | pPos, |
| const float & | pEpsilon = 0.0001f |
||
| ) |
Checks if the norm of a Position3D is near to 1.0
| pPos | the Position3D |
| pEpsilon | an optional epsilon distance |
| float AL::Math::norm | ( | const Rotation3D & | pRot | ) |
Compute the norm of a Rotation3D:
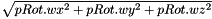
| pRot | the given Rotation3D |
| float AL::Math::norm | ( | const Quaternion & | pQua | ) |
Compute the norm of a Quaternion:
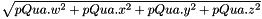
| pQua | the given Quaternion |
| float AL::Math::norm | ( | const Velocity3D & | pVel | ) |
Compute the norm of a Velocity3D:
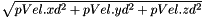
| pVel | the given Velocity3D |
| float AL::Math::norm | ( | const Velocity6D & | pVel | ) |
Compute the norm of a Velocity6D:
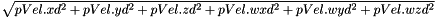
| pVel | the given Velocity6D |
| float AL::Math::norm | ( | const Position2D & | pPos | ) |
Compute the norm of a Position2D.
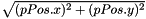
| pPos | the given Position2D |
| float AL::Math::norm | ( | const Position3D & | pPos | ) |
Compute the norm of a Position3D:
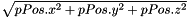
| pPos | the given Position3D |
| float AL::Math::norm | ( | const Position6D & | pPos | ) |
Compute the norm of a Position6D:
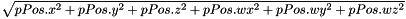
| pPos | the given Position6D |
| float AL::Math::norm | ( | const Transform & | pT | ) |
| Quaternion AL::Math::normalize | ( | const Quaternion & | pQua | ) |
| Velocity3D AL::Math::normalize | ( | const Velocity3D & | pVel | ) |
| Velocity6D AL::Math::normalize | ( | const Velocity6D & | pVel | ) |
| Position2D AL::Math::normalize | ( | const Position2D & | pPos | ) |
| Position3D AL::Math::normalize | ( | const Position3D & | pPos | ) |
| Position6D AL::Math::normalize | ( | const Position6D & | pPos | ) |
| void AL::Math::normalizeRotation | ( | Rotation & | pRot | ) |
| void AL::Math::normalizeTransform | ( | Transform & | pT | ) |
Normalize data, if needed, to have transform properties.
| pT | the given Transform |
| std::ostream& AL::Math::operator<< | ( | std::ostream & | pStream, |
| const Pose2D & | pPos | ||
| ) |
| std::ostream& AL::Math::operator<< | ( | std::ostream & | pStream, |
| const Position2D & | pPos | ||
| ) |
Overloading of operator << for Position2D.
| pStream | the given ostream |
| pPos | the given Position2D |
| std::ostream& AL::Math::operator<< | ( | std::ostream & | pStream, |
| const Position3D & | pPos | ||
| ) |
Overloading of operator << for Position3D.
| pStream | the given ostream |
| pPos | the given Position3D |
| std::ostream& AL::Math::operator<< | ( | std::ostream & | pStream, |
| const Position6D & | pPos | ||
| ) |
Overloading of operator << for Position6D.
| pStream | the given ostream |
| pPos | the given Position6D |
| std::ostream& AL::Math::operator<< | ( | std::ostream & | pStream, |
| const PositionAndVelocity & | pPosVel | ||
| ) |
Overloading of operator << for PositionAndVelocity.
| pStream | the given ostream |
| pPosVel | the given PositionAndVelocity |
| std::ostream& AL::Math::operator<< | ( | std::ostream & | pStream, |
| const Rotation & | pRot | ||
| ) |
| std::ostream& AL::Math::operator<< | ( | std::ostream & | pStream, |
| const Rotation3D & | pRot | ||
| ) |
Overloading of operator << for Rotation3D.
| pStream | the given ostream |
| pRot | the given Rotation3D |
| std::ostream& AL::Math::operator<< | ( | std::ostream & | pStream, |
| const Transform & | pT | ||
| ) |
| std::ostream& AL::Math::operator<< | ( | std::ostream & | pStream, |
| const TransformAndVelocity6D & | pTV | ||
| ) |
Overloading of operator << for TransformAndVelocity6D.
| pStream | the given ostream |
| pTV | the given TransformAndVelocity6D |
| std::ostream& AL::Math::operator<< | ( | std::ostream & | pStream, |
| const Velocity3D & | pVel | ||
| ) |
Overloading of operator << for Velocity3D.
| pStream | the given ostream |
| pVel | the given Velocity3D |
| std::ostream& AL::Math::operator<< | ( | std::ostream & | pStream, |
| const Quaternion & | pQua | ||
| ) |
Overloading of operator << for Quaternion.
| pStream | the given ostream |
| pQua | the given Quaternion |
| std::ostream& AL::Math::operator<< | ( | std::ostream & | pStream, |
| const Velocity6D & | pVel | ||
| ) |
Overloading of operator << for Velocity6D.
| pStream | the given ostream |
| pVel | the given Velocity6D |
| Pose2D AL::Math::pinv | ( | const Pose2D & | pPos | ) |
| Transform AL::Math::pinv | ( | const Transform & | pT | ) |
| Pose2D AL::Math::pose2dDiff | ( | const Pose2D & | pPos1, |
| const Pose2D & | pPos2 | ||
| ) |
| Pose2D AL::Math::pose2DInverse | ( | const Pose2D & | pPos | ) |
| void AL::Math::pose2DInverse | ( | const Pose2D & | pPos, |
| Pose2D & | pRes | ||
| ) |
| void AL::Math::pose2dInvertInPlace | ( | Pose2D & | pPos | ) |
| Quaternion AL::Math::quaternionFromAngleAndAxisRotation | ( | const float | pAngle, |
| const float | pAxisX, | ||
| const float | pAxisY, | ||
| const float | pAxisZ | ||
| ) |
Create a Quaternion initialized with explicit angle and axis rotation.
| pAngle | the float value for angle in radian around axis rotation |
| pAxisX | the float value for x value of axis rotation |
| pAxisY | the float value for y value of axis rotation |
| pAxisZ | the float value for z value of axis rotation |
| void AL::Math::quaternionInverse | ( | const Quaternion & | pQua, |
| Quaternion & | pQuaOut | ||
| ) |
Return the quaternion inverse of the given Quaternion:
| pQua | the given Quaternion |
| pQuaOut | the inverse of the given Quaternion |
| Quaternion AL::Math::quaternionInverse | ( | const Quaternion & | pQua | ) |
Return the quaternion inverse of the given Quaternion
| pQua | the given Quaternion |
| Rotation AL::Math::rotationFrom3DRotation | ( | const float & | pWX, |
| const float & | pWY, | ||
| const float & | pWZ | ||
| ) |
| Rotation AL::Math::rotationFromAngleDirection | ( | const float | pAngle, |
| const float | pX, | ||
| const float | pY, | ||
| const float | pZ | ||
| ) |
Creates a 3*3 Rotation Matrix from a an angle and a normalized direction( |pX, pY, pZ| = 1).
| pAngle | the float value of angle in radian |
| pX | the X direction of the vector of the rotation |
| pY | the Y direction of the vector of the rotation |
| pZ | the Z direction of the vector of the rotation |
| Rotation AL::Math::rotationFromQuaternion | ( | const float | pA, |
| const float | pB, | ||
| const float | pC, | ||
| const float | pD | ||
| ) |
Creates a 3*3 Rotation Matrix from a normalized quaternion ( |a + bi + cj + dk| = 1).
| pA | Coefficient a of the normalized quaternion |
| pB | Coefficient b of the normalized quaternion |
| pC | Coefficient c of the normalized quaternion |
| pD | Coefficient d of the normalized quaternion |
| Rotation AL::Math::rotationFromRotX | ( | const float | pRotX | ) |
| Rotation AL::Math::rotationFromRotY | ( | const float | pRotY | ) |
| Rotation AL::Math::rotationFromRotZ | ( | const float | pRotZ | ) |
| std::string AL::Math::toSpaceSeparated | ( | const Position3D & | pPos | ) |
| std::string AL::Math::toSpaceSeparated | ( | const Rotation3D & | pPos | ) |
| std::string AL::Math::toSpaceSeparated | ( | const Velocity6D & | pVel | ) |
| std::string AL::Math::toSpaceSeparated | ( | const Transform & | pT | ) |
| std::string AL::Math::toSpaceSeparated | ( | const Position6D & | pPos | ) |
| std::string AL::Math::toSpaceSeparated | ( | const Quaternion & | pQuat | ) |
Create a string of Quaternion.
<param name="pQuat> the given Quaternion
| Transform AL::Math::transformDiff | ( | const Transform & | pT1, |
| const Transform & | pT2 | ||
| ) |
| float AL::Math::transformDistance | ( | const Transform & | pT1, |
| const Transform & | pT2 | ||
| ) |
| float AL::Math::transformDistanceSquared | ( | const Transform & | pT1, |
| const Transform & | pT2 | ||
| ) |
| Transform AL::Math::transformFrom3DRotation | ( | const float & | pWX, |
| const float & | pWY, | ||
| const float & | pWZ | ||
| ) |
| Transform AL::Math::transformFromPosition | ( | const float & | pX, |
| const float & | pY, | ||
| const float & | pZ | ||
| ) |
| Transform AL::Math::transformFromPosition | ( | const float & | pX, |
| const float & | pY, | ||
| const float & | pZ, | ||
| const float & | pWX, | ||
| const float & | pWY, | ||
| const float & | pWZ | ||
| ) |
Create a Transform initialize with explicit value for translation part and euler angle:
H = fromRotZ(pWZ)*fromRotY(pWY)*fromRotX(pWX)
H.r1_c4 = pX
H.r2_c4 = pY
H.r3_c4 = pZ
| pX | the float value for translation axis x in meter (r1_c4) |
| pY | the float value for translation axis y in meter (r2_c4) |
| pZ | the float value for translation axis z in meter (r3_c4) |
| pWX | the float value for euler angle x in radian |
| pWY | the float value for euler angle y in radian |
| pWZ | the float value for euler angle z in radian |
| Transform AL::Math::transformFromRotX | ( | const float | pRotX | ) |
| Transform AL::Math::transformFromRotY | ( | const float | pRotY | ) |
| Transform AL::Math::transformFromRotZ | ( | const float | pRotZ | ) |
| void AL::Math::transformInverse | ( | const Transform & | pT, |
| Transform & | pTOut | ||
| ) |
| Transform AL::Math::transformInverse | ( | const Transform & | pT | ) |
| void AL::Math::transformInvertInPlace | ( | Transform & | pT | ) |
| void AL::Math::transformPreMultiply | ( | const Transform & | pT, |
| Transform & | pTOut | ||
| ) |
| void AL::Math::transformToFloatVector | ( | const Transform & | pT, |
| std::vector< float > & | pTOut | ||
| ) |
| std::vector<float> AL::Math::transformToFloatVector | ( | const Transform & | pT | ) |
| Rotation AL::Math::transpose | ( | const Rotation & | pRot | ) |
Compute the transpose rotation of the one given in argument:
| pRot | the rotation matrix |