A 3*3 rotation matrix.
More...
#include <alrotation.h>
|
| static Rotation | fromQuaternion (const float pA, const float pB, const float pC, const float pD) |
| | Creates a 3*3 Rotation Matrix from a normalized quaternion ( |a + bi + cj + dk| = 1). More...
|
| |
| static Rotation | fromAngleDirection (const float pAngle, const float pX, const float pY, const float pZ) |
| | Creates a 3*3 Rotation Matrix from a an angle and a normalized direction( |pX, pY, pZ| = 1). More...
|
| |
| static Rotation | fromRotX (const float pRotX) |
| | Create a Rotation initialized with explicit rotation around x axis. More...
|
| |
| static Rotation | fromRotXPi () |
| |
| static Rotation | fromRotY (const float pRotY) |
| | Create a Rotation initialized with explicit rotation around y axis. More...
|
| |
| static Rotation | fromRotYPi () |
| |
| static Rotation | fromRotZ (const float pRotZ) |
| | Create a Rotation initialized with explicit rotation around z axis. More...
|
| |
| static Rotation | fromRotZPi () |
| | Create a Rotation initialized with rotation of pi around z axis. More...
|
| |
| static Rotation | fromRotZHalfPi () |
| | Create a Rotation initialized with rotation of pi/2 around z axis. More...
|
| |
| static Rotation | from3DRotation (const float &pWX, const float &pWY, const float &pWZ) |
| | Create a Rotation initialized with euler angle. More...
|
| |
A 3*3 rotation matrix.
![$ \left[\begin{array}{ccc} r_1c_1 & r_1c_2 & r_1c_3 \\ r_2c_1 & r_2c_2 & r_2c_3 \\ r_3c_1 & r_3c_2 & r_3c_3 \end{array}\right]$](form_70.png)
more information
Definition at line 31 of file alrotation.h.
| AL::Math::Rotation::Rotation |
( |
| ) |
|
Create a Rotation initialized to identity.
![$ \left[\begin{array}{ccc} r_1c_1 & r_1c_2 & r_1c_3 \\ r_2c_1 & r_2c_2 & r_2c_3 \\ r_3c_1 & r_3c_2 & r_3c_3 \end{array}\right] = \left[\begin{array}{ccc} 1.0 & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 1.0 \end{array}\right]$](form_75.png)
| AL::Math::Rotation::Rotation |
( |
const std::vector< float > & |
pFloats | ) |
|
Create a Rotation with an std::vector.
- Parameters
-
| pFloats | An std::vector<float> of size 9, 12 or 16 for respectively: |
For std::vector<float> of size 9
![$ \left[\begin{array}{cccc} r_1c_1 & r_1c_2 & r_1c_3 \\ r_2c_1 & r_2c_2 & r_2c_3 \\ r_3c_1 & r_3c_2 & r_3c_3 \end{array}\right] = \left[\begin{array}{cccc} pFloats[0] & pFloats[1] & pFloats[2] \\ pFloats[3] & pFloats[4] & pFloats[5] \\ pFloats[6] & pFloats[7] & pFloats[8] \end{array}\right]$](form_76.png) For std::vector<float> of size 12 or 16:
For std::vector<float> of size 12 or 16: ![$ \left[\begin{array}{cccc} r_1c_1 & r_1c_2 & r_1c_3 \\ r_2c_1 & r_2c_2 & r_2c_3 \\ r_3c_1 & r_3c_2 & r_3c_3 \end{array}\right] = \left[\begin{array}{cccc} pFloats[0] & pFloats[1] & pFloats[2] \\ pFloats[4] & pFloats[5] & pFloats[6] \\ pFloats[8] & pFloats[9] & pFloats[10] \end{array}\right]$](form_77.png)
| float AL::Math::Rotation::determinant |
( |
| ) |
const |
Compute the determinant of the Rotation:
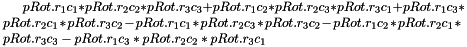
- Returns
- the float determinant of the Rotation
| static Rotation AL::Math::Rotation::from3DRotation |
( |
const float & |
pWX, |
|
|
const float & |
pWY, |
|
|
const float & |
pWZ |
|
) |
| |
|
static |
Create a Rotation initialized with euler angle.
Rot = fromRotZ(pWZ)*fromRotY(pWY)*fromRotX(pWX)
- Parameters
-
| pWX | the float value for euler angle x in radian |
| pWY | the float value for euler angle y in radian |
| pWZ | the float value for euler angle z in radian |
| static Rotation AL::Math::Rotation::fromAngleDirection |
( |
const float |
pAngle, |
|
|
const float |
pX, |
|
|
const float |
pY, |
|
|
const float |
pZ |
|
) |
| |
|
static |
Creates a 3*3 Rotation Matrix from a an angle and a normalized direction( |pX, pY, pZ| = 1).
- Parameters
-
| pAngle | the float value of angle in radian |
| pX | the X direction of the vector of the rotation |
| pY | the Y direction of the vector of the rotation |
| pZ | the Z direction of the vector of the rotation |
| static Rotation AL::Math::Rotation::fromQuaternion |
( |
const float |
pA, |
|
|
const float |
pB, |
|
|
const float |
pC, |
|
|
const float |
pD |
|
) |
| |
|
static |
Creates a 3*3 Rotation Matrix from a normalized quaternion ( |a + bi + cj + dk| = 1).
- Parameters
-
| pA | Coefficient a of the normalized quaternion |
| pB | Coefficient b of the normalized quaternion |
| pC | Coefficient c of the normalized quaternion |
| pD | Coefficient d of the normalized quaternion |
| static Rotation AL::Math::Rotation::fromRotX |
( |
const float |
pRotX | ) |
|
|
static |
Create a Rotation initialized with explicit rotation around x axis.
![$ pRot = \left[\begin{array}{cccc} 1.0 & 0.0 & 0.0 \\ 0.0 & cos(pRotX) & -sin(pRotX) \\ 0.0 & sin(pRotX) & cos(pRotX) \end{array}\right]$](form_72.png)
- Parameters
-
| pRotX | the float value for angle rotation in radian around x axis |
| static Rotation AL::Math::Rotation::fromRotXPi |
( |
| ) |
|
|
inlinestatic |
| static Rotation AL::Math::Rotation::fromRotY |
( |
const float |
pRotY | ) |
|
|
static |
Create a Rotation initialized with explicit rotation around y axis.
![$ pT = \left[\begin{array}{cccc} cos(pRotY) & 0.0 & sin(pRotY) \\ 0.0 & 1.0 & 0.0 \\ -sin(pRotY) & 0.0 & cos(pRotY) \end{array}\right]$](form_73.png)
- Parameters
-
| pRotY | the float value for angle rotation in radian around y axis |
| static Rotation AL::Math::Rotation::fromRotYPi |
( |
| ) |
|
|
inlinestatic |
| static Rotation AL::Math::Rotation::fromRotZ |
( |
const float |
pRotZ | ) |
|
|
static |
Create a Rotation initialized with explicit rotation around z axis.
![$ pT = \left[\begin{array}{cccc} cos(pRotZ) & -sin(pRotZ) & 0.0 \\ sin(pRotZ) & cos(pRotZ) & 0.0 \\ 0.0 & 0.0 & 1.0 \end{array}\right]$](form_74.png)
- Parameters
-
| pRotZ | the float value for angle rotation in radian around z axis |
| static Rotation AL::Math::Rotation::fromRotZHalfPi |
( |
| ) |
|
|
inlinestatic |
| static Rotation AL::Math::Rotation::fromRotZPi |
( |
| ) |
|
|
inlinestatic |
| bool AL::Math::Rotation::isNear |
( |
const Rotation & |
pRot2, |
|
|
const float & |
pEpsilon = 0.0001f |
|
) |
| const |
Check if the actual Rotation is near the one give in argument.
- Parameters
-
| pRot2 | the second Rotation |
| pEpsilon | an optionnal epsilon distance: default: 0.0001 |
- Returns
- true if the distance between the two rotations is less than pEpsilon
| bool AL::Math::Rotation::isRotation |
( |
const float & |
pEpsilon = 0.0001f | ) |
const |
Check if the rotation is correct. The condition checks are: 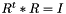 and determinant(R) = 1.0
and determinant(R) = 1.0
- Parameters
-
| pEpsilon | an optionnal epsilon distance. Default: 0.0001 |
- Returns
- true if the Rotation is correct
| void AL::Math::Rotation::normalizeRotation |
( |
void |
| ) |
|
Normalize data, if needed, to have Rotation properties.
| bool AL::Math::Rotation::operator!= |
( |
const Rotation & |
pRot2 | ) |
const |
Overloading of operator != for Rotation.
- Parameters
-
Overloading of operator * for Rotation.
- Parameters
-
Overloading of operator *= for Rotation.
- Parameters
-
| bool AL::Math::Rotation::operator== |
( |
const Rotation & |
pRot2 | ) |
const |
Overloading of operator == for Rotation.
- Parameters
-
| void AL::Math::Rotation::toVector |
( |
std::vector< float > & |
pReturnValue | ) |
const |
Return the Rotation as a vector of float:
![$ \begin{array}{cccc} [r_1c_1, & r_1c_2, & r_1c_3, \\ r_2c_1, & r_2c_2, & r_2c_3, \\ r_3c_1, & r_3c_2, & r_3c_3] \end{array}$](form_79.png)
| std::vector<float> AL::Math::Rotation::toVector |
( |
void |
| ) |
const |
| Rotation AL::Math::Rotation::transpose |
( |
| ) |
const |
Compute the rotation transpose (inverse) of the actual Rotation:
- Returns
- the Rotation transpose
| float AL::Math::Rotation::r1_c1 |
| float AL::Math::Rotation::r1_c2 |
| float AL::Math::Rotation::r1_c3 |
| float AL::Math::Rotation::r2_c1 |
| float AL::Math::Rotation::r2_c2 |
| float AL::Math::Rotation::r2_c3 |
| float AL::Math::Rotation::r3_c1 |
| float AL::Math::Rotation::r3_c2 |
| float AL::Math::Rotation::r3_c3 |
The documentation for this struct was generated from the following file:
- /home/opennao/work/release-2.8/lib/libalmath/almath/types/alrotation.h
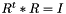 and determinant(R) = 1.0 More...
and determinant(R) = 1.0 More...![$ \left[\begin{array}{ccc} r_1c_1 & r_1c_2 & r_1c_3 \\ r_2c_1 & r_2c_2 & r_2c_3 \\ r_3c_1 & r_3c_2 & r_3c_3 \end{array}\right] = \left[\begin{array}{ccc} 1.0 & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 1.0 \end{array}\right]$](form_75.png)
![$ \left[\begin{array}{cccc} r_1c_1 & r_1c_2 & r_1c_3 \\ r_2c_1 & r_2c_2 & r_2c_3 \\ r_3c_1 & r_3c_2 & r_3c_3 \end{array}\right] = \left[\begin{array}{cccc} pFloats[0] & pFloats[1] & pFloats[2] \\ pFloats[3] & pFloats[4] & pFloats[5] \\ pFloats[6] & pFloats[7] & pFloats[8] \end{array}\right]$](form_76.png) For std::vector<float> of size 12 or 16:
For std::vector<float> of size 12 or 16: ![$ \left[\begin{array}{cccc} r_1c_1 & r_1c_2 & r_1c_3 \\ r_2c_1 & r_2c_2 & r_2c_3 \\ r_3c_1 & r_3c_2 & r_3c_3 \end{array}\right] = \left[\begin{array}{cccc} pFloats[0] & pFloats[1] & pFloats[2] \\ pFloats[4] & pFloats[5] & pFloats[6] \\ pFloats[8] & pFloats[9] & pFloats[10] \end{array}\right]$](form_77.png)
![$ pRot = \left[\begin{array}{cccc} 1.0 & 0.0 & 0.0 \\ 0.0 & cos(pRotX) & -sin(pRotX) \\ 0.0 & sin(pRotX) & cos(pRotX) \end{array}\right]$](form_72.png)
![$ pT = \left[\begin{array}{cccc} cos(pRotY) & 0.0 & sin(pRotY) \\ 0.0 & 1.0 & 0.0 \\ -sin(pRotY) & 0.0 & cos(pRotY) \end{array}\right]$](form_73.png)
![$ pT = \left[\begin{array}{cccc} cos(pRotZ) & -sin(pRotZ) & 0.0 \\ sin(pRotZ) & cos(pRotZ) & 0.0 \\ 0.0 & 0.0 & 1.0 \end{array}\right]$](form_74.png)
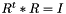 and determinant(R) = 1.0
and determinant(R) = 1.0 ![$ \begin{array}{cccc} [r_1c_1, & r_1c_2, & r_1c_3, \\ r_2c_1, & r_2c_2, & r_2c_3, \\ r_3c_1, & r_3c_2, & r_3c_3] \end{array}$](form_79.png)