|
libalmath
2.5.11.14a
|
|
libalmath
2.5.11.14a
|
A homogenous transformation matrix. More...
#include <altransform.h>
Public Member Functions | |
| Transform () | |
| Create a Transform initialized to identity. More... | |
| Transform (const std::vector< float > &pFloats) | |
| Create a Transform with an std::vector. More... | |
| Transform (const float &pPosX, const float &pPosY, const float &pPosZ) | |
| Create a Transform initialized with explicit value for translation part. Rotation part is set to identity. More... | |
| Transform & | operator*= (const Transform &pT2) |
| Overloading of operator *= for Transform. More... | |
| Transform | operator* (const Transform &pT2) const |
| Overloading of operator * for Transform. More... | |
| bool | operator== (const Transform &pT2) const |
| Overloading of operator == for Transform. More... | |
| bool | operator!= (const Transform &pT2) const |
| Overloading of operator != for Transform. More... | |
| bool | isNear (const Transform &pT2, const float &pEpsilon=0.0001f) const |
| Check if the actual Transform is near the one given in argument. More... | |
| bool | isTransform (const float &pEpsilon=0.0001f) const |
Check if the rotation part is correct. The condition checks are: 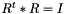 and determinant(R) = 1.0 More... and determinant(R) = 1.0 More... | |
| void | normalizeTransform (void) |
| Normalize data, if needed, to have transform properties. More... | |
| float | norm () const |
| Compute the norm translation part of the actual Transform: More... | |
| float | determinant () const |
| Compute the determinant of rotation part of the actual Transform: More... | |
| Transform | inverse () const |
| Compute the transform inverse of the actual Transform: More... | |
| Transform | diff (const Transform &pT2) const |
| Compute the Transform between the actual Transform and the one given in argument: More... | |
| float | distanceSquared (const Transform &pT2) const |
| Compute the squared distance between the actual Transform and the one given in argument (translation part): More... | |
| float | distance (const Transform &pT2) const |
| Compute the distance between the actual Transform and the one given in argument: More... | |
| void | toVector (std::vector< float > &pReturnVector) const |
| Return the Transform as a vector of float: More... | |
| std::vector< float > | toVector (void) const |
| void | writeToVector (std::vector< float >::iterator &pIt) const |
| Write the Transform in the vector and update the iterator: More... | |
Static Public Member Functions | |
| static Transform | fromRotX (const float pRotX) |
| Create a Transform initialized with explicit rotation around x axis. More... | |
| static Transform | fromRotY (const float pRotY) |
| Create a Transform initialized with explicit rotation around y axis. More... | |
| static Transform | fromRotZ (const float pRotZ) |
| Create a Transform initialized with explicit rotation around z axis. More... | |
| static Transform | from3DRotation (const float &pWX, const float &pWY, const float &pWZ) |
| Create a Transform initialize with euler angle. More... | |
| static Transform | fromPosition (const float pX, const float pY, const float pZ) |
| Create a Transform initialize with explicit value for translation part. More... | |
| static Transform | fromPosition (const float &pX, const float &pY, const float &pZ, const float &pWX, const float &pWY, const float &pWZ) |
| Create a Transform initialize with explicit value for translation part and euler angle. More... | |
| AL::Math::Transform::Transform | ( | ) |
Create a Transform initialized to identity.
![$ \left[\begin{array}{cccc} r_1c_1 & r_1c_2 & r_1c_3 & r_1c_4 \\ r_2c_1 & r_2c_2 & r_2c_3 & r_2c_4 \\ r_3c_1 & r_3c_2 & r_3c_3 & r_3c_4 \\ 0.0 & 0.0 & 0.0 & 1.0 \end{array}\right] = \left[\begin{array}{cccc} 1.0 & 0.0 & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \end{array}\right]$](form_97.png)
|
explicit |
Create a Transform with an std::vector.
| pFloats | An std::vector<float> of size 12 or 16 for respectively: |
![$ \left[\begin{array}{cccc} r_1c_1 & r_1c_2 & r_1c_3 & r_1c_4 \\ r_2c_1 & r_2c_2 & r_2c_3 & r_2c_4 \\ r_3c_1 & r_3c_2 & r_3c_3 & r_3c_4 \\ 0.0 & 0.0 & 0.0 & 1.0 \end{array}\right] = \left[\begin{array}{cccc} pFloats[00] & pFloats[01] & pFloats[02] & pFloats[03] \\ pFloats[04] & pFloats[05] & pFloats[06] & pFloats[07] \\ pFloats[08] & pFloats[09] & pFloats[10] & pFloats[11] \\ 0.0 & 0.0 & 0.0 & 1.0 \end{array}\right]$](form_98.png)
| AL::Math::Transform::Transform | ( | const float & | pPosX, |
| const float & | pPosY, | ||
| const float & | pPosZ | ||
| ) |
| float AL::Math::Transform::determinant | ( | ) | const |
| float AL::Math::Transform::distance | ( | const Transform & | pT2 | ) | const |
| float AL::Math::Transform::distanceSquared | ( | const Transform & | pT2 | ) | const |
|
static |
Create a Transform initialize with euler angle.
H = fromRotZ(pWZ)*fromRotY(pWY)*fromRotX(pWX)
| pWX | the float value for euler angle x in radian |
| pWY | the float value for euler angle y in radian |
| pWZ | the float value for euler angle z in radian |
|
static |
Create a Transform initialize with explicit value for translation part.
![$ pT = \left[\begin{array}{cccc} 1.0 & 0.0 & 0.0 & pX \\ 0.0 & 1.0 & 0.0 & pY \\ 0.0 & 0.0 & 1.0 & pZ \\ 0.0 & 0.0 & 0.0 & 1.0 \end{array}\right]$](form_105.png)
| pX | the float value for translation axis x in meter (r1_c4) |
| pY | the float value for translation axis y in meter (r2_c4) |
| pZ | the float value for translation axis z in meter (r3_c4) |
|
static |
Create a Transform initialize with explicit value for translation part and euler angle.
H = fromRotZ(pWZ)*fromRotY(pWY)*fromRotX(pWX)
then
H.r1_c4 = pX
H.r2_c4 = pY
H.r3_c4 = pZ
| pX | the float value for translation axis x in meter (r1_c4) |
| pY | the float value for translation axis y in meter (r2_c4) |
| pZ | the float value for translation axis z in meter (r3_c4) |
| pWX | the float value for euler angle x in radian |
| pWY | the float value for euler angle y in radian |
| pWZ | the float value for euler angle z in radian |
|
static |
Create a Transform initialized with explicit rotation around x axis.
![$ pT = \left[\begin{array}{cccc} 1.0 & 0.0 & 0.0 & 0.0 \\ 0.0 & cos(pRotX) & -sin(pRotX) & 0.0 \\ 0.0 & sin(pRotX) & cos(pRotX) & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \end{array}\right]$](form_102.png)
| pRotX | the float value for angle rotation in radian around x axis |
|
static |
Create a Transform initialized with explicit rotation around y axis.
![$ pT = \left[\begin{array}{cccc} cos(pRotY) & 0.0 & sin(pRotY) & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ -sin(pRotY) & 0.0 & cos(pRotY) & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \end{array}\right]$](form_103.png)
| pRotY | the float value for angle rotation in radian around y axis |
|
static |
Create a Transform initialized with explicit rotation around z axis.
![$ pT = \left[\begin{array}{cccc} cos(pRotZ) & -sin(pRotZ) & 0.0 & 0.0 \\ sin(pRotZ) & cos(pRotZ) & 0.0 & 0.0 \\ 0.0 & 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \end{array}\right]$](form_104.png)
| pRotZ | the float value for angle rotation in radian around z axis |
| Transform AL::Math::Transform::inverse | ( | ) | const |
| bool AL::Math::Transform::isNear | ( | const Transform & | pT2, |
| const float & | pEpsilon = 0.0001f |
||
| ) | const |
| bool AL::Math::Transform::isTransform | ( | const float & | pEpsilon = 0.0001f | ) | const |
Check if the rotation part is correct. The condition checks are: 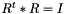 and determinant(R) = 1.0
and determinant(R) = 1.0
| pEpsilon | an optionnal epsilon distance. Default: 0.0001 |
| float AL::Math::Transform::norm | ( | ) | const |
| void AL::Math::Transform::normalizeTransform | ( | void | ) |
Normalize data, if needed, to have transform properties.
| bool AL::Math::Transform::operator!= | ( | const Transform & | pT2 | ) | const |
| bool AL::Math::Transform::operator== | ( | const Transform & | pT2 | ) | const |
| void AL::Math::Transform::toVector | ( | std::vector< float > & | pReturnVector | ) | const |
Return the Transform as a vector of float:
![$ \begin{array}{cccc} [r_1c_1, & r_1c_2, & r_1c_3, & r_1c_4, \\ r_2c_1, & r_2c_2, & r_2c_3, & r_2c_4, \\ r_3c_1, & r_3c_2, & r_3c_3, & r_3c_4, \\ 0.0, & 0.0, & 0.0, & 1.0] \end{array}$](form_86.png)
| std::vector<float> AL::Math::Transform::toVector | ( | void | ) | const |
| void AL::Math::Transform::writeToVector | ( | std::vector< float >::iterator & | pIt | ) | const |
Write the Transform in the vector and update the iterator:
![$ \begin{array}{cccc} [r_1c_1, & r_1c_2, & r_1c_3, & r_1c_4, \\ r_2c_1, & r_2c_2, & r_2c_3, & r_2c_4, \\ r_3c_1, & r_3c_2, & r_3c_3, & r_3c_4, \\ 0.0, & 0.0, & 0.0, & 1.0] \end{array}$](form_86.png) is assumed the vector has enough space.
is assumed the vector has enough space.