|
libalmath
2.4.3.28-r2
|
It aims to control a position and/or rotation of a part of the robot in natural 3D space. There are different mathematical ways to represent the position and the orientation of a rigid body in space. ALMath offers two ways to represent a solid in 3D:
At the end of this section, we describe how to compute the transform from a position6D.
Rotation matrix In our case, a rotation matrix is a 3*3 matrix. In linear algebra, a rotation matrix is a matrix that applies a rotation in Euclidean space.
![$ R = \left[\begin{array}{ccc} r_1c_1 & r_1c_2 & r_1c_3 \\ r_2c_1 & r_2c_2 & r_2c_3 \\ r_3c_1 & r_3c_2 & r_3c_3 \\ \end{array}\right]$](form_121.png) with
with 
The following three basic rotation matrices rotate vectors around x, y or z axis, in three dimensions.
![$ R_x(\theta) = \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & cos(\theta) & -sin(\theta) \\ 0 & sin(\theta) & cos(\theta) \\ \end{array}\right]$](form_123.png)
![$ R_y(\theta) = \left[\begin{array}{ccc} cos(\theta) & 0 & sin(\theta) \\ 0 & 1 & 0 \\ -sin(\theta) & 0 & cos(\theta) \\ \end{array}\right]$](form_124.png)
![$ R_z(\theta) = \left[\begin{array}{ccc} cos(\theta) & -sin(\theta) & 0 \\ sin(\theta) & cos(\theta) & 0 \\ 0 & 0 & 1 \end{array}\right]$](form_125.png)
Transform: Homogeneous representation
The homogenous representation is a 4*4 matrix which is composed of rotation and translation part. It represent a solid in 3D.
![$ H = \left[\begin{array}{cc} R & r \\ 0_{1,3} & 1 \end{array}\right]$](form_126.png)
with:
![$\left[r_x r_y r_z\right]^t $](form_127.png) : translation part
: translation part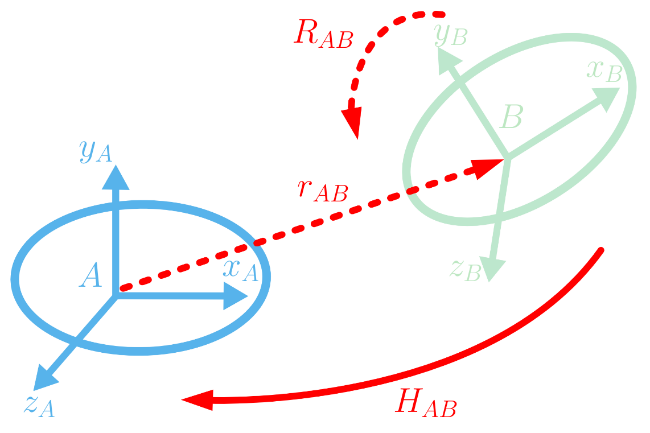
![$ H_{ab} = \left[\begin{array}{cc} R_{ab} & r_{ab} \\ 0_{1,3} & 1 \end{array}\right]$](form_128.png)
![$ H_{ba} = H_{ab}^{-1} = \left[\begin{array}{cc} R_{ab}^t & -R_{ab}^t r_{ab} \\ 0_{1,3} & 1 \end{array}\right]$](form_129.png)
Position6D
A Position6D is a vector of 6 dimensions composed of 3 translations (in meters) and 3 rotation (in radians). The angle convention of Position6D is 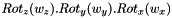 .
.
![$ Position6D = \left[\begin{array}{c} x \\ y \\ z \\ w_x \\ w_y \\ w_z \end{array}\right]$](form_131.png)
with:
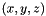 : translation part (3 scalars)
: translation part (3 scalars)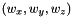 : rotation part (3 scalars)
: rotation part (3 scalars)Position6D versus Transform
The following equation shows how to compute a transform from a position6D.
![$ Position6D = \left[\begin{array}{c} x \\ y \\ z \\ w_x \\ w_y \\ w_z \end{array}\right]$](form_131.png) =>
=> ![$ H = \left[\begin{array}{cc} R & r \\ 0_{1,3} & 1 \end{array}\right]$](form_126.png) with
with ![$ \left\{\begin{array}{l} R = R_z(w_z) R_y(w_y) R_x(w_x) \\ r = \left[\begin{array}{ccc}x & y & z \end{array}\right]^t \end{array}\right.$](form_134.png)
Basic Example: represente a solid which position is x=1.0, y=-0.5, z=0.4 ad his orientation is 10 degree around x axis. 10 degree is equal to 0.1745 radian. In this basic case, it is very simple to use Position6D.
![$ Position6D = \left[\begin{array}{c} +1.0 \\ -0.5 \\ -0.4 \\ 0.1745 \\ 0.0 \\ 0.0 \end{array}\right]$](form_135.png) <=>
<=> ![$ Transform = \left[\begin{array}{cccc} 1 & 0 & 0 & +1.0 \\ 0 & 0.9848 & -0.1736 & -0.5 \\ 0 & 0.1736 & 0.9848 & +0.4 \\ 0 & 0 & 0 & 1 \end{array}\right]$](form_136.png)